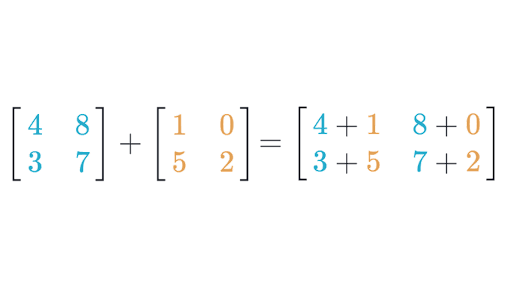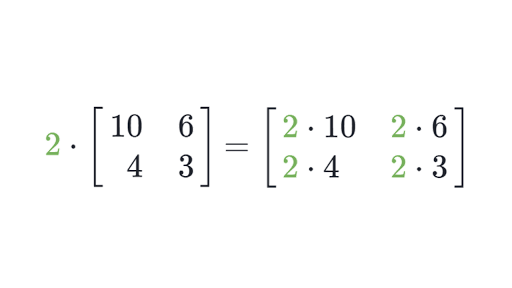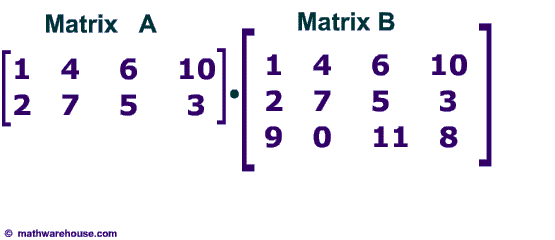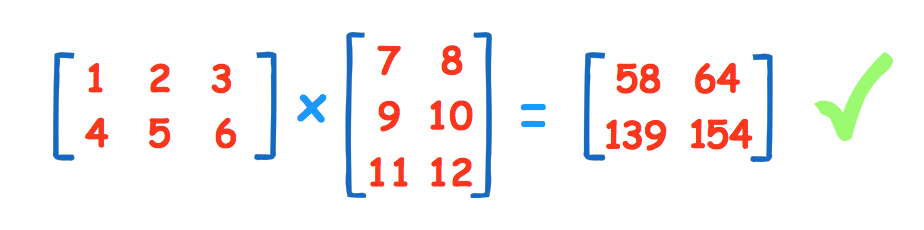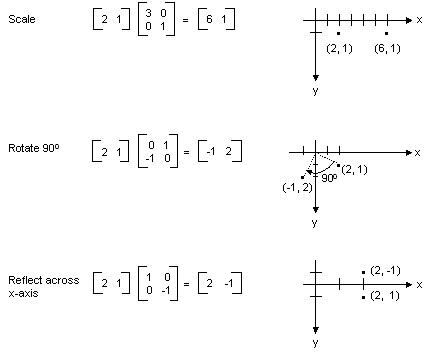E-journal 6: An Act of Coordinate Violence

“The introduction of numbers as coordinates is an act of violence.”

Hermann Weyl, Philosophy of Mathematics and Natural Science

Part 1

Hermann Weyl must’ve struggled to comprehend that topic you have in your textbook about using matrices to transform a shape, because he doesn’t seem too pleased about matrix transformations, at least judging from the quote above.

While Hermann Weyl could’ve wailed all he wanted about his mathematical and philosophical woes, however, we 14-15-year-olds have an IGCSE to face that will definitely have at least one question about matrix transformations. So, how do we do it?

Matrices

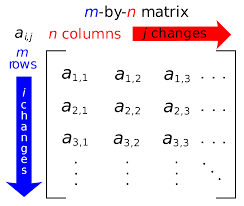
A matrix is a rectangular array of numbers or other mathematical objects for which operations such as addition and multiplication are defined.

We can see the order of a matrix (row by column) from the above picture.

Operations

The operations we can do with a matrix at IGCSE level includes the following:
– Addition
– Subtraction
– Multiplication by Scalar
– Multiplying Matrices
– “Division”

Adding Matrices

As you can see, adding matrices is pretty simple. We simply add numbers in the same position together. In the above example, the sum of the numbers 4 and 1, both at the top, leftmost spot in their respective matrices, is the top, leftmost number in the new, resultant sum matrix.

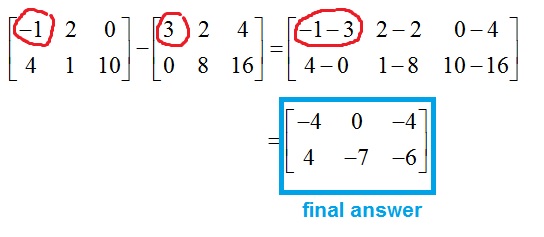
Subtracting Matrices

The concept stays the same for subtracting matrices; simply subtract numbers in the same position together. For example, the difference between the numbers -1 and 3, both at the top, leftmost spot in their respective matrices, is -4, which is placed at the top, leftmost number in the new, resultant matrix.

Multiplication by Scalar

Multiplication by scalar is a little different. Here, the scalar (the constant, which is 2 in this case) by every number in the matrix to get the resultant matrix.

Multiplying Matrices

Multiplying matrices is where I believe Weyl’s brain began its road to hell, though it doesn’t have to be the same for you, reader.

First, there is a condition that needs to be fulfilled for multiplying between matrices to happen. The number of columns the first matrix must be the same as the number of rows of the second matrix; or (the matrices need to have the orders of AxB and BxC respectively in that order). This means that matrices like these:

which have the orders of 2×4 and 3×4 respectively, can’t be multiplied.

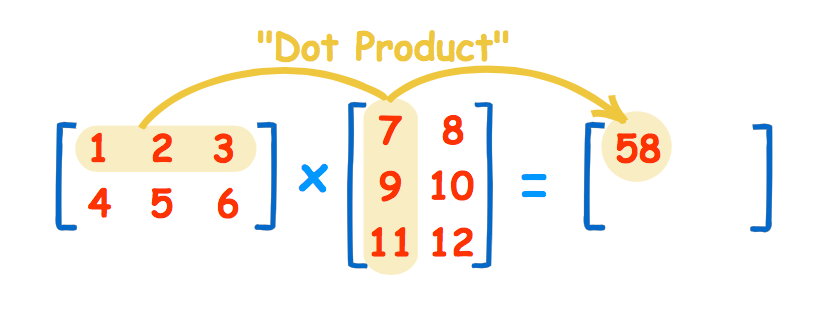
Now, we need to find the dot product of the rows and columns, which essentially mean this:

In this particular example, we need to do the dot product 4 times, till we get this:

This is a formula we can use, which is admittedly more complicated than the above method but you can use if it’s easier for you:

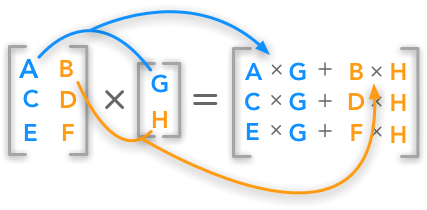
The placement of the dot products is from left to right from top to bottom, just like how we read.

Note that matrix multiplication is not commutative. In other words, the order of the matrices matter since AxB is not equal to BxA, unless…

one of the matrices is an identity matrix, which is:

– a square matrix (same number of columns as rows)
– all numbers are 0
– except for numbers that are part of the principal diagonal, which is a diagonal line from top, leftmost to bottom, rightmost.

This is an identity matrix:

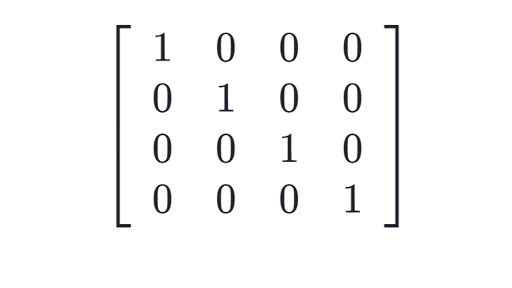
Any matrix multiplied by the identity matrix will result in the same initial matrix.

“Division”

When I say divide, I don’t really mean divide, rather I mean multiplying with a matrix’s inverse. Like this:

Matrices can also have an inverse if they’re
– not singular
– a square matrix.

Singular matrices are matrices whose determinant is 0. The determinant of a matrix depends on its order. For IGCSE level, we only need to be able to find the determinant of matrices whose orders are 2×2 and 3×3, like such:

The formula for a matrix’s inverse is this:

For IGCSE level, we only need to know the inverse of a 2×2 matrix.

Transformations

Now, as you’ve probably guessed, matrices can represent coordinates. But how can these simple arrays of numbers possibly represent coordinates on a 2-D plane or even transform them?

Well, like this:

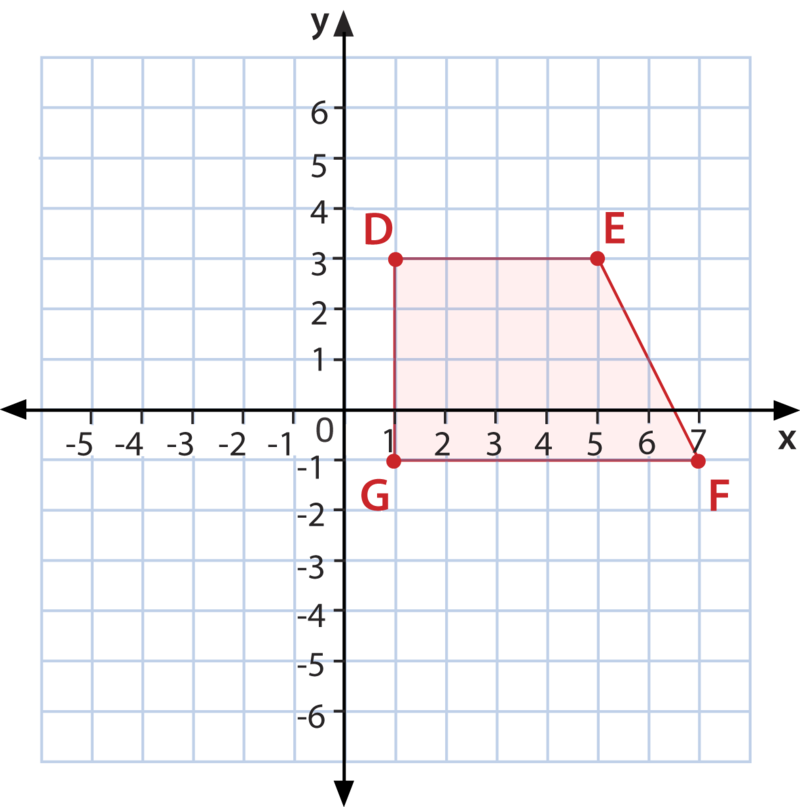
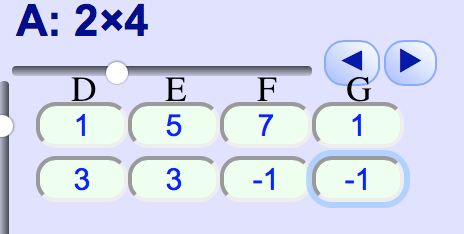
The top row represents the x-axis and the bottom row the y-axis.
Column 1 represents the coordinates of point D, column 2 the coordinates of point E and so on.

Coordinate matrices don’t necessarily have to form shapes. They may just be the matrix of a coordinate. Nonetheless, these matrices can still be transformed.

Transformations

There are 4 types of transformations:
– Rotation
– Translation
– Reflection
– Enlargement

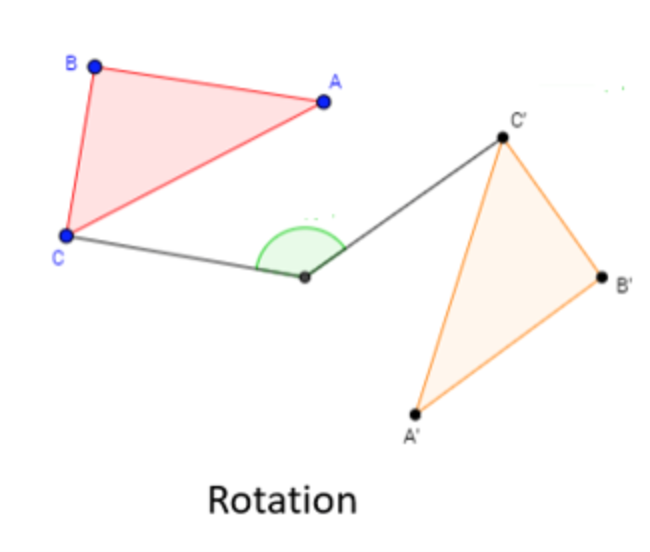
Rotation
If an object is ‘rotated’, this means that it is turned a specific number of degrees around a centre point.

Translation
If an object is ‘translated’ this means that it is moved up, down, left or right of its original position on a grid. When translating an object, its shape size and direction remain the same.

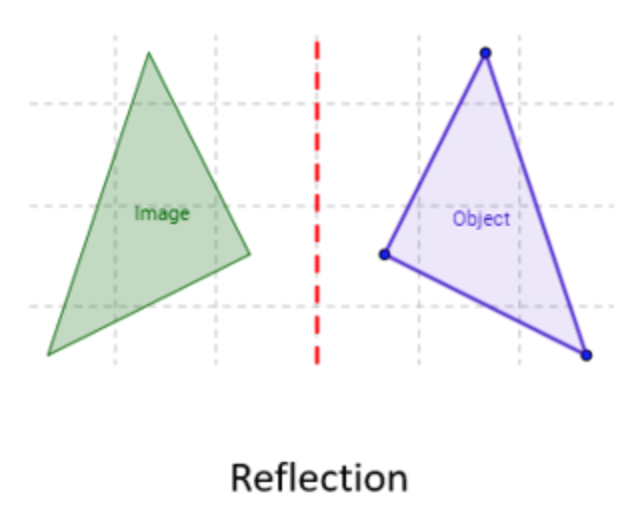
Reflection
If an image is ‘reflected’, this means that it faces the opposite direction of the original object.

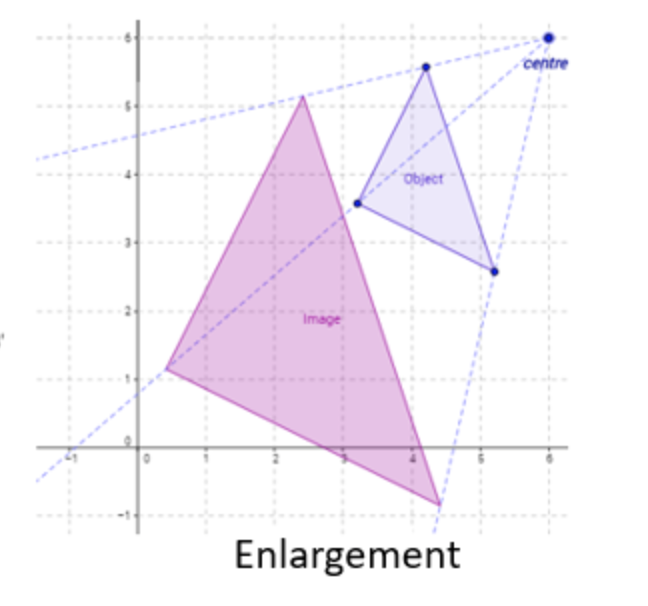
Enlargement
If you ‘enlarge’ or ‘resize’ an object, this means that you change its size but keep its original shape the same. In order to carry out enlargements, you need to know the scale factor of the object and the centre of enlargement.

Matrix Transformation

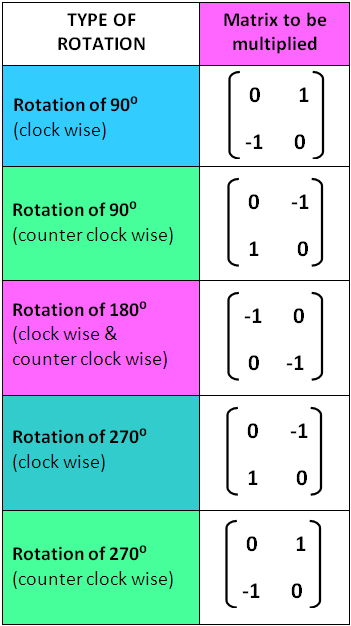
Now, there are ways to transform a coordinate matrix by multiplying it with other, specific matrices.

Here’s the list:

You may wonder why these specific matrices can transform coordinate matrices. Well, the best answer I can give you is that these matrices are all based on the identity matrix, just with some negatives and changing around in places. If you multiply one of these matrices with a coordinate matrix, I can guarantee you the resultant coordinate matrix will form a shape that is the original shape from the original coordinate matrix transformed.

Part 2

Uses of Matrices and Tranformations

Matrices are used in real life to render video game visuals since graphics software use matrices to process linear transformations to render images.

Matrices are also used by engineers in order to model physics systems and find the accurate result for complex calculations to allow machinery to work.

Transformations more specifically, on the other hand, are used in the mass production of glasses. After all, we need reflection to ensure the two sides of spectacles are symmetrical since even the smallest degree of imbalance can cause great discomfort to the wearer.

Part 3

IB Learners are knowledgable and reflective individuals. Through this e-journal, I was able to reflect on the ideas I absorbed during class and think on how I can apply them and solve problems with them. With this lesson, I increase my knowledge on maths and the limits of my math capabilities expands. I can show this by critically thinking and answering math problems with these new concepts in mind.