Ejournal 5: It is … Probably.

“I believe that we do not know anything for certain, but everything probably.” 

–Christiaan Huygens

Part 1

In so many things in life, it can’t be helped that we aren’t 100% sure of what will happen. So many are the unknown unknowns and the unknown knowns that at best, we can only say that something will happen … probably. Luckily, math, as our usual reliably torturous subject, does away with all the uncertainty and allows us to calculate the probability of a certain event happening.

Before we delve too deeply into probability, however, lets reflect on sets.

Sets

A set is a collection or group of distinct objects. Some examples of sets include:

A = {x : x is a positive odd number less than 10}

Then A = {1, 3, 5, 7, 9}

B is the set of days in a week.

Then B = {Monday, Tuesday, Wednesday, Thursday, Friday, Saturday, Sunday}

The objects in a set are known as elements of the set. For example, in the above examples I gave, 1, 3, 5, 7, 9 are all members of set A. This can be written in set notation as 3∈A (3 is a member of A).

Sets can also be empty of null, represented by the set notations ∅ and {}.

Sets can also be universal, wherein a set contains all possible elements. For example, a set of real numbers could be the universal set of a set of even numbers.

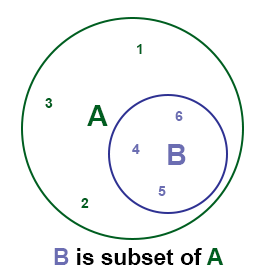
Sets can have subsets. This means that the members of the set and subset overlap as seen below.

You can see a more complete explanation for all the set notation symbols below.

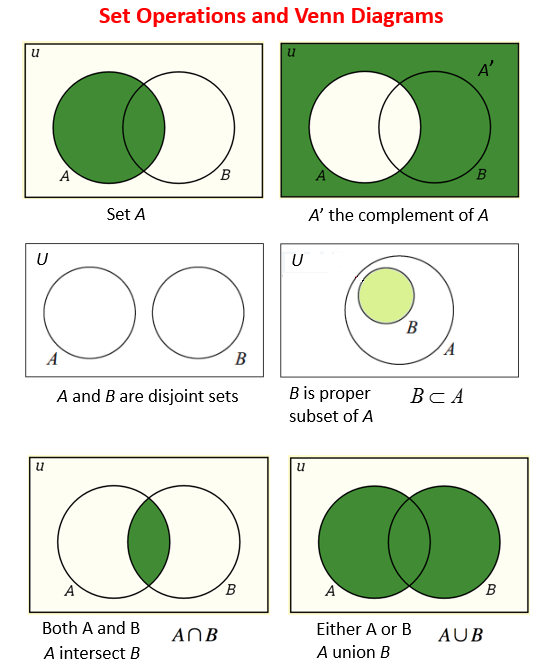
These set notations and the sets themselves can then be show in the form of Venn diagrams.

Probability

Probability is a branch of mathematics that allows us to analyze random experiments. In other words, if we’re given data on the number of students wearing glasses, not wearing glasses, are female and are male, we can reasonably get the probability of the likeliness of getting a male student who wears glasses if we picked a random student from the class.

In probability, a 0 means that an event won’t happen – it is impossible – and a 1 means the opposite – it will definitely happen. All probabilities lie between these two numbers, in fraction or decimal.

Below are some probability formulas.

Mutually exclusive events mean that the two events are, in reference to a venn diagram, disjoint or have no intersection. Non-mutual events or combined events are events where the two events do have an intersection (hence why in the above formula the intersection of A and B was subtracted; to prevent overlap of members).

Conditional probability is the likeliness of one event occurring with some relationship to one or more other events.

For example, we have a deck of cards (typical), and draw two cards without returning any. We want to calculate the probability of drawing a Jack the first draw and drawing another Jack the next draw.

For the first draw, the probability of drawing a Jack is 4/52.

P(A)=4/52

Since we don’t return the cards, for the second draw, the likeliness of drawing a Jack becomes 3/51.

In set notation, this can be written as:

P(A and B) = P(A) x P(B|A) = (4/52) x (3/51) = 12/2652 = 1/221

We can depict probability by using tree diagrams, like in the below example of a tree diagram for the probabilities of a coin flip.

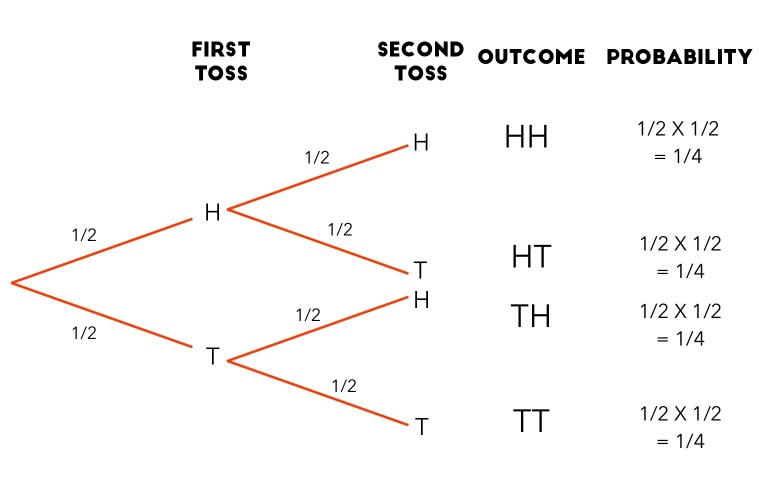
Tree diagrams allow us to easily see the probability of singular events (the numbers on the branches), but aren’t convenient for questions with many outcomes (draws/tosses).

Sometimes you may also be asked for the relative frequency of an event. Do not fear, this just means the question is asking you for the probability of that event in percentage of decimal form.

Part 2

Uses of Sets and Probability

Since sets are just a collection or group of distinct objects, the real life uses of sets is more to just describing of what is in a certain group.

For example, a spotify playlist titled ‘Women of K-Pop’ would include songs made by Korean female soloists or groups in the pop genre and would not include blues songs.

Another example is that a school bag has different pockets for different objects. The biggest, middle division would be for textbooks, notebooks and any other bulkier objects while the front pocket would be for thinner, less essential objects like earphones.

Probability plays a large role in analysing insurance policies to decide which insurance most suits your needs. If your city is rampant with crimes and the local government publishes a study where, in your city, every 1 in 3 men can expect to experience an attempted assault on themselves once every 3 months, you would purchase an insurance that caters to this need. In other words, probability can help us make decisions.

While it is unfortunate and mildly depressing to know that life is almost entirely out of our control, calculating simpler probabilities can help us get a better grasp of what happens around us (and maybe win us some card games). Either way, enjoy life and know that one definite thing you can count on is life being unpredictable … probably.